- 0 Posts
- 10 Comments
this is a surface integral so the joke is (loosely): as opposed to peeling in straight strips (line integral), grandma is peeling continuously without lifting her hand

 6·5 days ago
6·5 days agolol 98 million? why not something proportional to the ad revenue that apple made in said years? oh I know why because law exists for billionaires. this is just apple paying some more money so that this scandal goes away as soon as possible which might be even more costly to them on the long run than the 98 mil they are paying.

 3·5 days ago
3·5 days agohe is ultra rich, the hateful divide and conquer tactics applied to common people don’t apply to him so he simply does not have any empathy for the matter.

 22·6 days ago
22·6 days agoperhaps executives are more replaceable by AI than workers are?

 132·9 days ago
132·9 days agoAchieving a velocity of 0.5 times the speed of light (ccc) for space travel involves solving advanced challenges in physics and engineering. The Python script below creates a simplified optimization framework to analyze the propulsion needed. It uses physics principles like relativistic mass-energy equivalence and propulsion mechanisms such as fusion or antimatter engines.
This code assumes you have the theoretical fuel and energy to achieve the speed, but it abstracts away complex challenges like time dilation, cosmic radiation, and material limitations.
Python Code
import numpy as np import matplotlib.pyplot as plt # Constants c = 3e8 # Speed of light (m/s) target_speed = 0.5 * c # Target speed (0.5c) ship_mass = 1e5 # Mass of the spacecraft without fuel (kg) fuel_efficiency = 1e-3 # Fuel conversion efficiency (e.g., antimatter ~0.1, fusion ~0.001) exhaust_velocity = 1e7 # Exhaust velocity of the propulsion system (m/s) specific_impulse = exhaust_velocity / 9.81 # Specific impulse (seconds) # Functions def relativistic_mass(speed, rest_mass): """Calculate relativistic mass.""" gamma = 1 / np.sqrt(1 - (speed / c) ** 2) return gamma * rest_mass def fuel_needed(final_speed, ship_mass, exhaust_velocity): """Estimate fuel required using the Tsiolkovsky rocket equation.""" delta_v = final_speed mass_ratio = np.exp(delta_v / exhaust_velocity) fuel_mass = ship_mass * (mass_ratio - 1) return fuel_mass # Optimization def optimize_propulsion(target_speed, ship_mass, exhaust_velocity, fuel_efficiency): fuel_mass = fuel_needed(target_speed, ship_mass, exhaust_velocity) energy_required = fuel_mass * fuel_efficiency * c**2 # Total energy for propulsion return fuel_mass, energy_required # Perform calculations fuel_mass, energy_required = optimize_propulsion(target_speed, ship_mass, exhaust_velocity, fuel_efficiency) # Display results print(f"Target speed: {target_speed / c:.2f}c") print(f"Required fuel mass: {fuel_mass:.2e} kg") print(f"Energy required: {energy_required:.2e} joules") # Visualization speeds = np.linspace(0, 0.5 * c, 100) fuel_masses = [fuel_needed(speed, ship_mass, exhaust_velocity) for speed in speeds] plt.figure(figsize=(10, 6)) plt.plot(speeds / c, fuel_masses, label='Fuel Mass Required') plt.xlabel('Speed as a Fraction of Light Speed (v/c)') plt.ylabel('Fuel Mass (kg)') plt.title('Fuel Requirement vs. Speed') plt.legend() plt.grid() plt.show()How it Works:
Relativistic Mass: Accounts for relativistic effects as the spacecraft approaches significant fractions of the speed of light. Tsiolkovsky Rocket Equation: Estimates fuel requirements based on the propulsion system's exhaust velocity and initial mass. Energy Requirement: Evaluates energy needs assuming the specified fuel efficiency.Limitations:
Idealized Assumptions: Assumes perfect efficiency and ignores engineering constraints. Simplified Physics: Doesn't account for external factors like gravity, drag, or realistic propulsion systems. Energy Storage: No consideration for how energy would be stored or delivered.Would you like more refinement or details on specific subsystems?
FIRE ALL THE PHYSICISTS
surprisingly many computational scientists use MacOS
The one which has the high approval rate has a very good working relationship with billionaires which kisses the government’s feet, the type of government we will be seeing in the USA for the next four years.

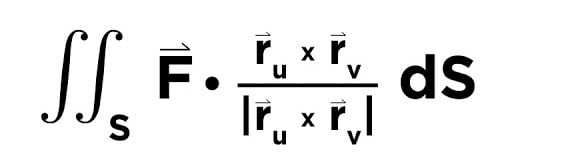


how do you know a scammer? from his desire to run a large bitcoin operation. examples: Trump, Elon, Tate, Nigel. Surprised? I am not.